事情是这样的,我在社区看到了一个帖子,《来做道炉石数学题!》https://www.iyingdi.com/tz/post/5208573
这里分享一下我的解题思路。
首先我把原题搬过来:
问题
对面只剩1血,场上有7个满血的詹姆斯,这时打出可以造成28伤害的多拿寿司大帝,消灭对手的概率是?
分析
首先我们对游戏机制做出以下假设:
- 大帝不会攻击已经死亡的詹姆斯。
- 在每次攻击前,场上每一个存活的目标受到这次攻击的概率是相等的。
核心思路
因此我们可以计算每一**击之后的多有情况以及对应的关系,并用这一轮的概率递推出下一轮的概率,直到得到第28次攻击也就是28轮之后的各种情况的概率。
也就是说我们首先要找到表示场上每一种情况的方法,以及递推的方法。
首先,我们自然的能想到可以用一个长度为7的数组表示场上7个詹姆斯的血量情况,再用一个整数表示英雄的血量。这样就能表示所有的情况了。
然后递推的方法也呼之欲出
一开始(第0轮)只存在一种情况,即英雄血量为1,詹姆斯血量分别为4,4,4,4,4,4,4该情况的概率为1
那么在第二轮,这个第一轮的唯一的情况将会将自己所有的概率1,平均分给由它自身衍生出的各种情况。假设能衍生出n种情况,就是每种新情况各自增加1/n 在这里因为所有单位都还存活所以n为8 也就是说n其实就是当前情况下血量不为0的单位的个数
以此类推,第二轮的各种情况也会衍生出第三轮的情况,直到求得最终解。
问题简化
思路有了,但该问题还可以进一步简化。因为在我们的假设中,每一轮中各个尚且存活的单位承受攻击的概率是相等的,那么意味着其实各个詹姆斯的占位对最终结果的计算是没有影响的。也就是说4,4,4,4,4,4,0的情况和0,4,4,4,4,4,4的情况是可以归为一种的。在表示情况的时候先对詹姆斯的血量进行排序就可以减少一部分不必要的情况。
解答
我们可以用string表示每种情况,用哈希表来储存各种情况对应的概率,然后动态规划就完事了
废话不多说,直接上具体的c++实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<unordered_map>
#include<string>
#include<vector>
#include <algorithm>
using namespace std;
class Solution{
public:
shared_ptr<unordered_map<string, double>> dp;
shared_ptr<unordered_map<string, double>> dp_next;
Solution(){
dp=make_shared<unordered_map<string, double>>();
dp_next=make_shared<unordered_map<string, double>>();
}vector<int> split(const string& str) {
vector<int> res;
if("" == str) return res;
char * strs = new char[str.length() + 1] ;
strcpy(strs, str.c_str());
char *p = strtok(strs,"-");
while(p) {
string s = p;
res.push_back(stoi(s));
p = strtok(NULL, "-");
}
return res;
}void encode(string &str, const vector<int>&James, const int Hero){
vector<int>James_ordered(James.begin(),James.end());
sort(James_ordered.begin(),James_ordered.end(),greater<int>());
char buffer[20];
sprintf_s(buffer,"%d-%d-%d-%d-%d-%d-%d-%d",Hero,James[0],James[1],James[2],James[3],James[4],James[5],James[6]);
str=string(buffer);
}void decode(string str, vector<int>&James, int &Hero){
vector<int>temp=split(str);
Hero=temp[0];
for(int i=0;i<7;++i){
James[i]=temp[i+1];
}
}void add_to_next(const vector<int>&James,const int &Hero,const double p){
string temp;
vector<int>James_next(James.begin(),James.end());
int count = 0;//统计目前还没噶的有几个 再计算概率
if (Hero == 1) {
count++;
}
for(int i=0;i<7;++i){
if(James[i]>0){
count++;
}
}
double add_p = p / count;
if (Hero == 1) {
encode(temp,James,Hero-1);
(*dp_next)[temp]=(*dp_next)[temp]+add_p;
}
for(int i=0;i<7;++i){
if(James[i]>0){
James_next[i]=James_next[i]-1;
encode(temp,James_next,Hero);
James_next[i]=James_next[i]+1;
(*dp_next)[temp]=(*dp_next)[temp]+add_p;
}
}}
void run(){
vector<int>James(7,4);
int Hero=1;
(*dp)[string("1-4-4-4-4-4-4-4")] = 1.0;
for(int round=1;round<=29;++round){
cout<<"round:"<<round<<" ";
dp_next->clear();
for (auto &one : *dp){
decode(one.first,James,Hero);
add_to_next(James,Hero,one.second);
}
swap(dp,dp_next);
// get result
double alive=0;
for (auto &one : *dp){
decode(one.first,James,Hero);if(Hero==1){
alive+=one.second;
}
}
cout<<"alive:"<<alive<<endl;
}
}
};int main(){
auto s= Solution();
s.run();
system("pause");
return 0;
}
结论
最终存活概率为0.286827%
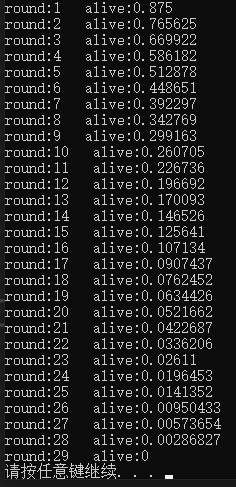

代码有问题可以评论区讨论。如果你有更优的解法也欢迎评论区分享你的思路。
最重要的是,我好久没写c++,写的不好的地方还请各位海涵。

















































